Week 3: Control Flow
Exercise #3.1 Harmonic Numbers
Harmonic numbers are a sequence of numbers that
arises in various fields of mathematics. The n-th
harmonic number, denoted as Hn, is defined as the sum
of the reciprocals of the first n natural numbers: %20(2).png) Write a Java program
HarmonicNumber that on input a positive integer n,
prints the n -th harmonic number.
Write a Java program
HarmonicNumber that on input a positive integer n,
prints the n -th harmonic number.
Test case 1:
| Input: | Output: |
|---|---|
| 2 | 1.5 |
Test case 2:
| Input: | Output: |
|---|---|
| 10 | 2.9289682539682538 |
My code:
1 | |
Exercise #3.2 Black Jack
In Black Jack card game, we call a value busts if it exceeds
a sum of 21. Write a Java program BlackJack that on input 2
integer values greater than 0, prints a single integer of whichever
value is nearest to 21 without going bust. Print -1 if both values bust.

For example:
| Input | Result |
|---|---|
| 20 19 | 20 |
| 19 22 | 19 |
| 22 23 | 1 |
My code:
1 | |
Exercise #3.3 Pandemic Spread
Write a Java program PandemicSpread to simulate how fast a pandemic spread with the following input: init : the initial number of infected persons on day 1numInfect : the average number of healthy people that one infected person newly infects per daypopulation : the total number of people in the areaReturn the day on which the entire population will be infected.
For example:
| Input | Result |
|---|---|
| 1 2 10 | 4 |
| 5 3 1000 | 5 |
My code:
1 | |
Exercise #3.4 Right Triangle
Write a Java program RightTriangle that takes three integer input
numbers and determines whether they make up the side lengths of a right
triangle . 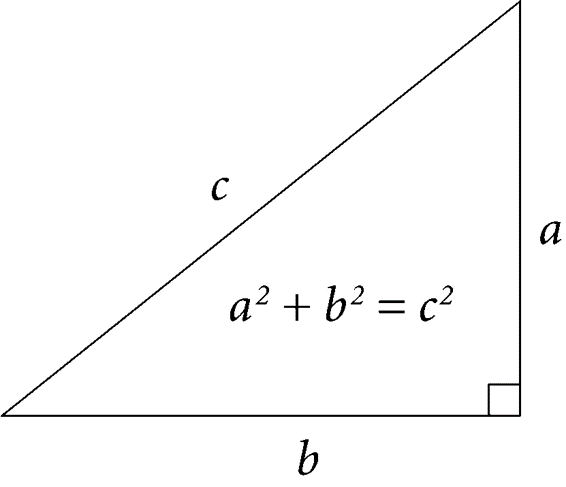
Your program must print output true if and only if the following two conditions are true :
- All three integers are positive (greater than zero).
- You can find two integers where the sum of the squares of those two integers is equal to the square of the third integer.
For example:
| Input | Result |
|---|---|
| 5 12 13 | true |
| 5 4 3 | true |
| -3 -4 5 | false |
My code:
(a bit strange tho, but it works)
1 | |
Lab Exercise #3.1 Armstrong Number
An Armstrong number is an n-digit number that equals the sum of the nth power of its digits. For example,
- 153 is a three-digit number where the sum of the cubes of the individual digits equal
- 1634 is a four-digit number where the sum of the 4th power of the
individual digits equal 1634
.png)
Write a Java program Armstrong that on input two positive integers a and k, prints the first k Armstrong numbers greater than or equal to a.
For example:
| Input | Result |
|---|---|
| 100 2 | 153 370 |
| 1500 1 | 1634 |
My code:
1 | |
Lab 3 Challenge - Hailstone Sequence Length
The Hailstone sequence is computed as follows:
- Start with an integer number nIf n is even, the next number in the sequence is n/2
- If n is odd, the next number is 3n+1
- Continue until it reaches 1For example, for n = 3, the sequence is 3, 10, 5, 16, 8, 4, 2, 1 and for n = 12, the sequence is 12, 6, 3, 10, 5, 16, 8, 4, 2, 1

Write a Java program HailStone that on input a positive integer n, prints the length of the Hailstone sequence starting at n.
Note that, interestingly, we still do not know whether the Hailstone sequence will ever reaches 1 for all starting n ! This is also known in the literature as the Collatz conjecture.
For example:
| Input | Result |
|---|---|
| 3 | 8 |
| 12 | 10 |
My code:
1 | |


